Chapter 8 Logistic Regression (W7)
8.1 What is a Logistic Regression?
- 로지스틱 회귀분석은 Y값이 0이나 1인 특수한 선형 모형
- 참조: [위키피디아]
8.2 Linear Regression (W5) vs. Logistic Regression (W7)
- Linear Regression: Predict continuous variables ‘Y’
- 수업 성적 (백분율 점수): Y값은 78, 99, 69, 100…
- Logistic Regression: Predict binary classification
- 수업의 성적 (Pass/Fail): Y값은 둘 중에 하나이다 –> Pass(1) or Fail(0),
- Y값이 0이나 1만 있을 경우 그래프는 S 모양으로 나타남
- 로지스틱 회귀분석은 S모양을 선형으로 나타내기 위해서 종속변수(Y) 에 logit 변환을 적용하는 것임
8.3 Logistic Regression
- 오즈 (odds): 성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타냄
- 축구: 한국이 모로코를 이길 확률이 0.2이고 질 확률이 0.8이다
- odds = 0.2/0.8 = 0.25
- 도박의 기준이다 (한국에 이긴다를 2만원을 걸면 8만원을 딸 수 있다)
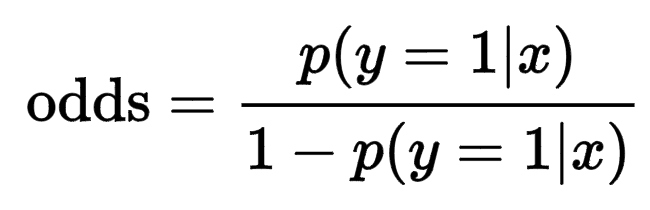
Figure 8.1: odds
로짓변환: 오즈에 로그를 취한 함수로서 입력 값의 범위가 [-무한대 ,+무한대] 일 때 출력 값의 범위를 [0,1]로 조정함

Figure 8.2: logit
8.4 Function (함수)
- glm(formula,data,family)
- glm(종속변수~독립변수, 데이터, family = binomial)
- glm: Generalized Linear Model의 약자
- family = binomial: 로지스틱회귀분석을 할때 사용
- summary()로 결과 출력mtcars 데이터 불러오기 (4개의 컬럼을 불러옴 (am, cyl, hp, wt))
- mtcars 데이터는 R에 내장이 되어 있으며, 자동차 모델별로 다양한 스펙을 담고 있음 [mtcars 데이터정보]
- am: automatic (0: auto, 1: manual)
- syl: 실린더, 몇 기통인가?
- hp: horsepower, 마력
- wt: weight, 무게
- vs: V engine or S engine (0: V, 1: S)
- mpg: Miles/(US) gallon (차량의 연료소비)
8.4.1 예제
모든 컬럼 출력 (원하는 컬럼만 출력을 하려면 subset을 사용할 수도 있다)
data(mtcars)
myData <- mtcars
# myData <- subset(mtcars, select=c(mpg, am, vs)) #원하는
# 컬럼만 출력하고 싶을 때
myData## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160.0 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160.0 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108.0 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258.0 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360.0 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225.0 105 2.76 3.460 20.22 1 0 3 1
## Duster 360 14.3 8 360.0 245 3.21 3.570 15.84 0 0 3 4
## Merc 240D 24.4 4 146.7 62 3.69 3.190 20.00 1 0 4 2
## Merc 230 22.8 4 140.8 95 3.92 3.150 22.90 1 0 4 2
## Merc 280 19.2 6 167.6 123 3.92 3.440 18.30 1 0 4 4
## Merc 280C 17.8 6 167.6 123 3.92 3.440 18.90 1 0 4 4
## Merc 450SE 16.4 8 275.8 180 3.07 4.070 17.40 0 0 3 3
## Merc 450SL 17.3 8 275.8 180 3.07 3.730 17.60 0 0 3 3
## Merc 450SLC 15.2 8 275.8 180 3.07 3.780 18.00 0 0 3 3
## Cadillac Fleetwood 10.4 8 472.0 205 2.93 5.250 17.98 0 0 3 4
## Lincoln Continental 10.4 8 460.0 215 3.00 5.424 17.82 0 0 3 4
## Chrysler Imperial 14.7 8 440.0 230 3.23 5.345 17.42 0 0 3 4
## Fiat 128 32.4 4 78.7 66 4.08 2.200 19.47 1 1 4 1
## Honda Civic 30.4 4 75.7 52 4.93 1.615 18.52 1 1 4 2
## Toyota Corolla 33.9 4 71.1 65 4.22 1.835 19.90 1 1 4 1
## Toyota Corona 21.5 4 120.1 97 3.70 2.465 20.01 1 0 3 1
## Dodge Challenger 15.5 8 318.0 150 2.76 3.520 16.87 0 0 3 2
## AMC Javelin 15.2 8 304.0 150 3.15 3.435 17.30 0 0 3 2
## Camaro Z28 13.3 8 350.0 245 3.73 3.840 15.41 0 0 3 4
## Pontiac Firebird 19.2 8 400.0 175 3.08 3.845 17.05 0 0 3 2
## Fiat X1-9 27.3 4 79.0 66 4.08 1.935 18.90 1 1 4 1
## Porsche 914-2 26.0 4 120.3 91 4.43 2.140 16.70 0 1 5 2
## Lotus Europa 30.4 4 95.1 113 3.77 1.513 16.90 1 1 5 2
## Ford Pantera L 15.8 8 351.0 264 4.22 3.170 14.50 0 1 5 4
## Ferrari Dino 19.7 6 145.0 175 3.62 2.770 15.50 0 1 5 6
## Maserati Bora 15.0 8 301.0 335 3.54 3.570 14.60 0 1 5 8
## Volvo 142E 21.4 4 121.0 109 4.11 2.780 18.60 1 1 4 2myLogit <- glm(vs ~ mpg, data = myData, family = binomial)
summary(myLogit) #결과출력##
## Call:
## glm(formula = vs ~ mpg, family = binomial, data = myData)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2127 -0.5121 -0.2276 0.6402 1.6980
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.8331 3.1623 -2.793 0.00522 **
## mpg 0.4304 0.1584 2.717 0.00659 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 43.860 on 31 degrees of freedom
## Residual deviance: 25.533 on 30 degrees of freedom
## AIC: 29.533
##
## Number of Fisher Scoring iterations: 6- P-value (유의확률)이 0.001 미만으로 나타나 mpg가 VS (엔진유형)에 유의미한 영향을 미치는 것으로 판단이 됨
- P-value는 낮을 수록 좋고, 별이 한개(0.01 미만)라도 있어야 유의하다는 것임.
- 결과출력이 알아서 별을 붙이므로, 별이 한개면 P-value가 0.01 미만이므로, 별이 2개면 P-value가 0.001 미만이므로 x가 y에 유의미한 영향을 미치는 것으로 판단이 된다는 식으로 설명하면 됨
- 별이 없다면 x가 y에 유의미한 영향을 미치는 것이 않는다고 해석하면 됨
- mpg가 1증가함에 따라 S 엔진일 확률이 V 엔진일 확률보다 0.4304배가 커짐
library(ggplot2)
ggplot(myData, aes(x = mpg, y = vs)) + geom_point() + stat_smooth(method = "glm",
method.args = list(family = "binomial"), se = FALSE)