Chapter 6 Simple Linear Regression (W5-1)
6.1 What is a Regression?
- 회귀분석(Regression)이란? 위키피디아
- 변수와 변수와의 관계를 봐서 값을 예측하는 통계방법 (원인과 결과)
- A –> B (A가 B에 영향을 끼치는 것)
- y = ax + b
- 독립변수(Independent variable): x이며 y 값에 영향을 주는 변수
- 종속변수(Dependent variable): y이며 분석대상이 되는 변수
- 회귀분석의 목적
- 회귀분석의 종류
- 단순회귀분석: 종속변수 1개, 독립변수도 1개
- 다중회귀분석: 종속변수 1개, 독립변수는 2개 이상
- 단순회귀분석이 해석이 쉽고 명확하지만 종속변수를 1개의 독립변수로 설명하기 어렵다는 한계를 가짐
6.2 Simple Linear Regression
- 단순선형회귀(Simple Linear Regression)란?
- In statistics, simple linear regression is a linear regression model with a single explanatory variable.That is, it concerns two-dimensional sample points with one independent variable and one dependent variable and finds a linear function… [위키피디아(영어)]
- 사용할 함수
- lm(formula,data)
- lm은 선형모델 (linear model)의 약자
- 데이터
- 키: 151, 174, 138, 186, 128, 136, 179, 163, 152, 131
- 몸무게: 63, 81, 56, 91, 47, 57, 76, 72, 62, 48
- 단순선형회귀 공식
- y = ax + b
- 몸무게 = a(키) + b
- x, y는 어떻게 선택하는가?
- 알려고 하는 것이 y이다
- 우리는 몸무게를 알고 싶다
- (예. 키가 175이면 몸무게가 몇일가?)
- y = ax + b
6.3 예제
키와 몸무게의 관계를 보기 위해 회귀분석을 해보자
- x(키)와 y(몸무게)에 데이터를 넣고
- abline(): 직선그리기
- plot을 사용하여 그래프를 그린다
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131) # 키입력
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48) # 몸무게 입력
# lm() 함수적용
myLM <- lm(y ~ x) # myLM에 함수를 적용한 것을 저장
summary(myLM) # 결과 출력##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.3002 -1.6629 0.0412 1.8944 3.9775
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -38.45509 8.04901 -4.778 0.00139 **
## x 0.67461 0.05191 12.997 1.16e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.253 on 8 degrees of freedom
## Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
## F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06- P-value (유의확률)이 0.00 미만으로 나타나 키가 몸무게에 유의미한 영향을 미치는 것으로 판단이 됨
- P-value는 낮을 수록 좋고, 별이 한개(0.01 미만)라도 있어야 유의하다는 것임.
- 결과출력이 알아서 별을 붙이므로, 별이 한개면 P-value가 0.01 미만이므로, 별이 2개면 P-value가 0.001 미만이므로 x가 y에 유의미한 영향을 미치는 것으로 판단이 된다는 식으로 설명하면 됨
- 별이 없다면 x가 y에 유의미한 영향을 미치는 것이 않는다고 해석하면 됨
- 키가 1cm 커짐에 따라 몸무게가 0.67461kg 늘어남
회귀직선 그리기
plot(x, y, ylab = "Weight", xlab = "Height") # 그래프 그리기, 라벨 추가
abline(myLM) # 위에서 그린 plot에 직선그리기
- 잔차 표준오차(Residual standard error)
- 잔차 표준오차 : 3.253
- 잔차란? y값과 추정된 y값과의 차이
- 즉 이 모형으로 키로부터 몸무게를 예측했을 때 평균 3.23kg의 오차가 생긴다는 의미
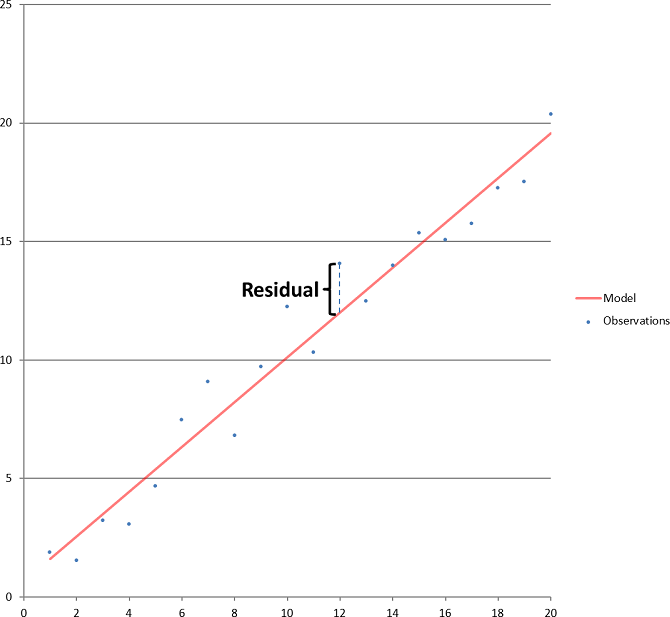
Figure 6.1: Data Structure
- R-Square(결정계수): 모델의 설명력 –> 설명력이 높다 낮다의 의미
- 0에 가까우면 독립변수는 종속변수를 잘 예측할 수 없다는 의미
- 1에 가까우면 독립변수는 종속변수를 잘 예측할 수 있다는 의미 (1이면 오차없이 예측가능하다)
- 0.9548 –> 독립변수가(키, x)가 종속변수(몸무게, y)의 설명을 95.48% 할 수 있다
- Coefficients
- Intercept: 절편
- x 값이 0일 경우의 y값
- -38.45509 (키가 0이면 몸무게는 -38.45509이다, 키가 0일수는 없지만 분석결과처럼 선을 그리면 그렇다는 의미)
- 기울기: 0.67461
- Intercept: 절편
- y=0.6741x - 38.45509
- p-value
- 일반적으로 0.5보다 작으면 유의하다 (학문의 분야나 방법론에 따라 0.1, 0.01, 0.001 등을 사용하기도 함)
- ’키는 몸무게에 영향을 준다’라고 주장했는데, 이것이 아닐 확률
모델에 따르면 키가 174 이면 몸무게가 몇일까?
y <- 0.6741 * 174 - 38.45509
y## [1] 78.83831