Chapter 7 Multiple Linear Regression (W5-2)
7.1 What is a Regression?
- 회귀분석(Regression)이란? 위키피디아
- 변수와 변수와의 관계를 봐서 값을 예측하는 통계방법 (원인과 결과)
- A –> B (A가 B에 영향을 끼치는 것)
- y = ax + b
- 독립변수(Independent variable): x이며 y 값에 영향을 주는 변수
- 종속변수(Dependent variable): y이며 분석대상이 되는 변수
- 회귀분석의 목적
- 회귀분석의 종류
- 단순회귀분석: 종속변수 1개, 독립변수도 1개
- 다중회귀분석: 종속변수 1개, 독립변수는 2개 이상
- 단순회귀분석이 해석이 쉽고 명확하지만 종속변수를 1개의 독립변수로 설명하기 어렵다는 한계를 가짐
7.2 Multiple Linear Regression (다중 선형회귀)
- 다중 선형회귀(Multiple Linear Regression)란?
7.3 예제 (mtcars)
variables
- 종속변수(y) 독립변수(x)
- y => mpg
- x1 => cyl
- x2 => disp
- x3 => hp
- x4 => drat
- x5 => wt
data(mtcars)
head(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1그래프로 데이터 확인
- 눈짐작으로 상관관계가 있는가?
- 상관관계가 있으려면 점이 어떻게 찍혀야 하는가?
library(ggplot2) #Load package ggplot2 to use function qplot
qplot(cyl, wt, data = mtcars)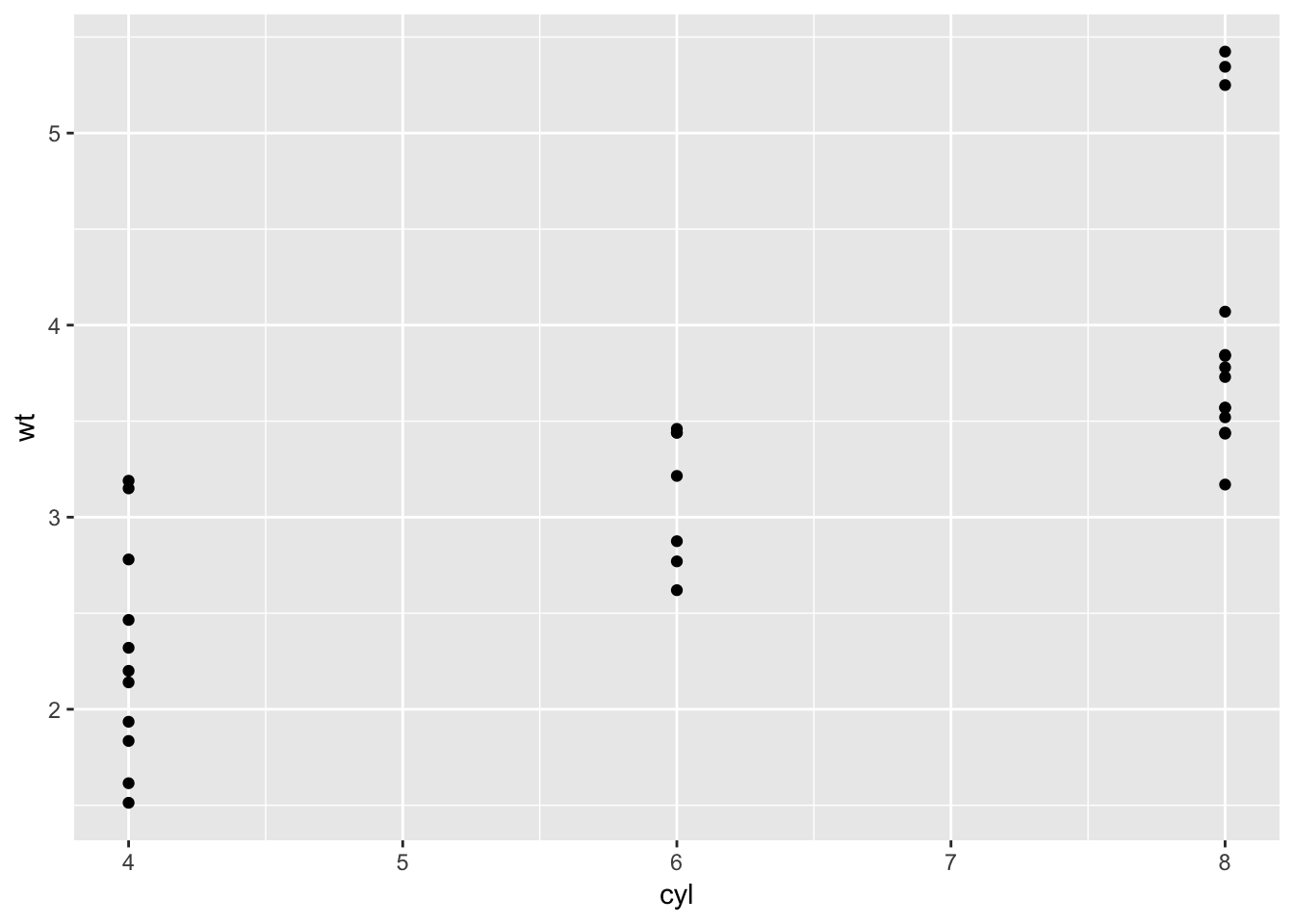
Mymtcars <- mtcars[, c(1:6)]
pairs(Mymtcars, panel = panel.smooth)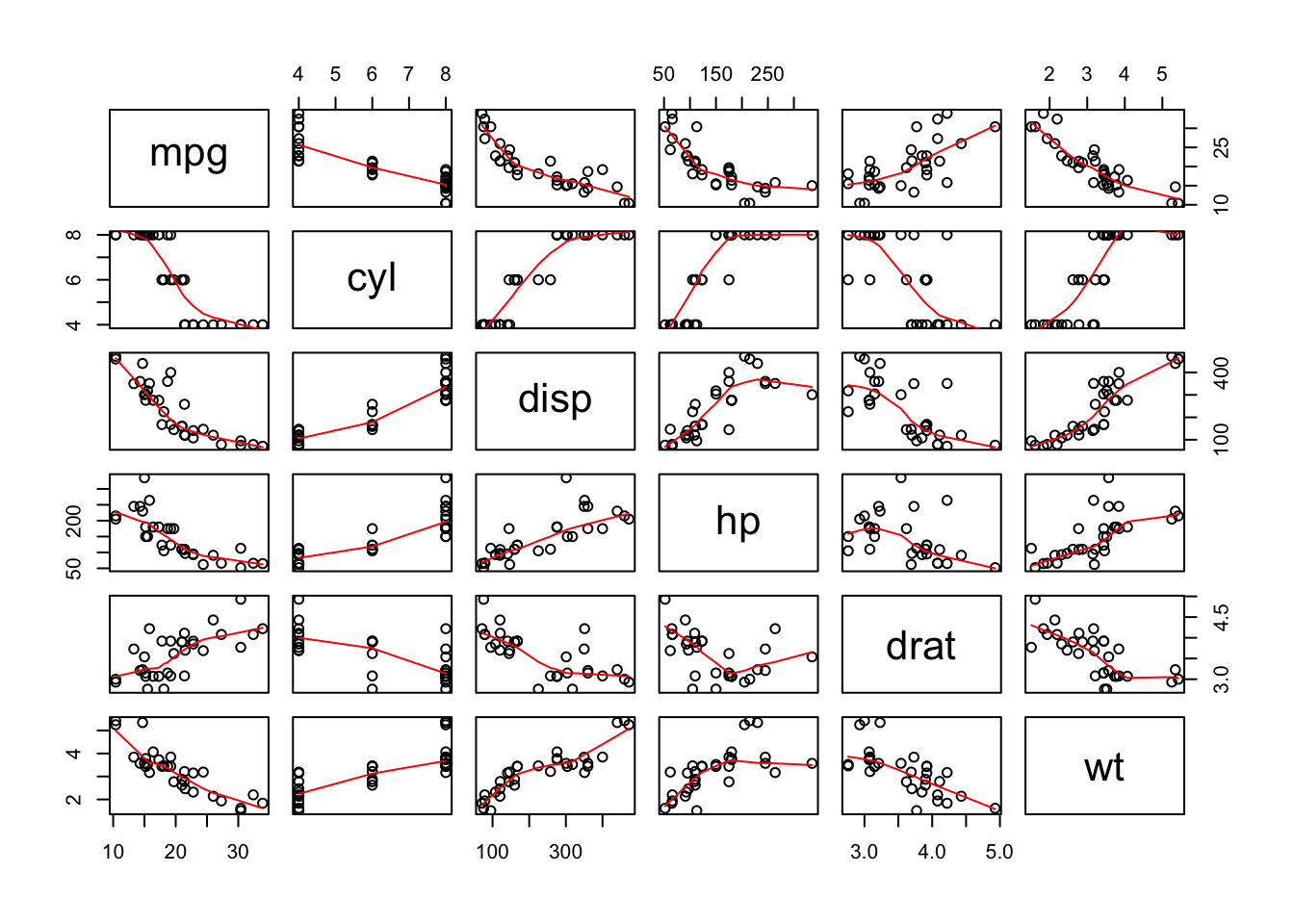
cor(Mymtcars[, -1])## cyl disp hp drat wt
## cyl 1.0000000 0.9020329 0.8324475 -0.6999381 0.7824958
## disp 0.9020329 1.0000000 0.7909486 -0.7102139 0.8879799
## hp 0.8324475 0.7909486 1.0000000 -0.4487591 0.6587479
## drat -0.6999381 -0.7102139 -0.4487591 1.0000000 -0.7124406
## wt 0.7824958 0.8879799 0.6587479 -0.7124406 1.0000000correlation (상관관계)
- x1, x2, x3는 독립변수들이다
- 왜 독립변수라고 하는가?
- 서로 독립적이어야 한다
- 즉, 서로 상관관계가 없어야 한다
- 예를 들면, x1 = 발크기, x2 = 손크기 로 변수들을 정하면?
- 둘의 상관성이 크므로, 제대로 된 결과가 안나온다
- 그러므로 둘중 한개만 선택해야 한다
- 상관관계측정 하는 법
- 대표적으로 pearson, kendall, spearman 3가지 방법이 있다
- 옵션을 넣어서 선택하거나 여러개 출력 가능, method = c(“pearson”, “kendall”, “spearman”)
- cor(mtcar[,-5], method = c(“spearman”))
- 기본은 pearson이므로 옵션을 무시해도 됨
- cor() 함수를 사용하여 상관관계 분석
- cor(mtcar[,-5]): 5번째 컬럼만 제외 (1,2,3,4)
- cor(mtcar[,1:4]): 첫번째 컬럼부터 4번째 컬럼까지 (1,2,3,4)
- -0.6보다 높거나, 0.6보다 낮아야 함 (연구분야에 따라 다름, 0.5, 0.7로도 정함)
두 변수간의 상관관계
cor(Mymtcars[, -1])## cyl disp hp drat wt
## cyl 1.0000000 0.9020329 0.8324475 -0.6999381 0.7824958
## disp 0.9020329 1.0000000 0.7909486 -0.7102139 0.8879799
## hp 0.8324475 0.7909486 1.0000000 -0.4487591 0.6587479
## drat -0.6999381 -0.7102139 -0.4487591 1.0000000 -0.7124406
## wt 0.7824958 0.8879799 0.6587479 -0.7124406 1.0000000Multicollinearity: 다중공선성 체크
- 두개 이상의 독립변수들간의 상관관계
- 10 이상 이면 그 변수는 제거
- vif() 함수 –> library(car)를 불러와야 함
- vif(variance inflation factor) = 분산팽창계수
library(car)
model <- lm(mpg ~ cyl + disp + hp + drat + wt, data = Mymtcars)
summary(model)##
## Call:
## lm(formula = mpg ~ cyl + disp + hp + drat + wt, data = Mymtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7014 -1.6850 -0.4226 1.1681 5.7263
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.00836 7.57144 4.756 6.4e-05 ***
## cyl -1.10749 0.71588 -1.547 0.13394
## disp 0.01236 0.01190 1.039 0.30845
## hp -0.02402 0.01328 -1.809 0.08208 .
## drat 0.95221 1.39085 0.685 0.49964
## wt -3.67329 1.05900 -3.469 0.00184 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.538 on 26 degrees of freedom
## Multiple R-squared: 0.8513, Adjusted R-squared: 0.8227
## F-statistic: 29.77 on 5 and 26 DF, p-value: 5.618e-10vif(model)## cyl disp hp drat wt
## 7.869010 10.463957 3.990380 2.662298 5.168795- 결과 해석
- Intercept는 모든 변수가 없을 경우의 기본값입니다 (36.00836)
- 저번 수업에 설명한 오늘의 기분(y)에 영향을 미치는 원인 (x1=날씨, x2=수면량, x3=교통체증)에 빗대어 생각을 해봅시다
- y = ax1 + bx2 + cx3 + d
- intercept는 d에 해당하며, 날씨 수면량, 교통체증과 상관없이 기본적인 나의 기분을 뜻합니다.
- a, b, c는 기울기이므로 위결과에서 estimated coefficients (-1.10749, 0.01236, -0.02402. 0.95221, -3.67329)에 해당합니다. (위의 결과는 자동차에 관한 데이터라, 수업시간에 제가 예로 기분에 대한 데이터가 아님)
- P값의 유의한 것은 signifi. codes를 보면 됨
- 별 3개 2개 1개가 유의한거로 보세요
- 점(.)으로 된것은 marginal 하다는 것인데 (0.1 미만), 유의하지 않은 것으로 해석을 하세요 (수업시간에 제가 점을 별로 봐서 두 변수가 유의하다고 설명을 한 듯함)
- 즉, 위에서는 wt변수(**)만 유의하고, drat(.)은 유의하지 않습니다.
- 그리고 disp변수는 vif는 10이상이니, 빼야 하는 변수 입니다
- 즉 disp를 빼고 회귀분석을 다시 돌려야 함
- lm(formula = mpg ~ cyl + hp + drat + wt, data = Mymtcars)
- Intercept는 모든 변수가 없을 경우의 기본값입니다 (36.00836)